Voici un objet qui défie autant vos yeux que votre calculatrice préférée. À la sortie de sa boite, comme tant d’autres avant vous, vous vous imaginez voguant sur les mers recherchant une île au trésor par le petit bout de la lorgnette.

 Mais pour votre plus grand malheur, cet objet n’est pas équipé de verres grossissants, mais d’un supercalculateur portatif fonctionnant avec l’énergie sans limites de votre poignet.
Mais pour votre plus grand malheur, cet objet n’est pas équipé de verres grossissants, mais d’un supercalculateur portatif fonctionnant avec l’énergie sans limites de votre poignet.
J’arrête là le suspens, vous tenez dans vos mains une règle à calculer. Cet instrument est capable de multiplier à très grande vitesse, de diviser, d’élever au carré, ou au cube, de trouver les racines carrées et cubiques, les sinus et cosinus et bien d’autres fonctions encore, tout ceci avec un rouleau de papier annoté, une partie coulissante et un curseur.
Mais comment un simple bout de papier peut-il faire ce que des générations d’ordinateurs se sont vues incapables de réaliser ?

Exactement comme d’autres générations de cancres se sont vues réussir aux examens ; en trichant ! !
En effet, toutes les solutions sont indiquées sur ce rouleau ; il suffit ainsi, pour trouver la réponse adéquate, de savoir utiliser cet objet légalement utilisé par tous les ingénieurs depuis Napoléon.
Pour ce faire, il suffit de savoir l’opération que nous voulons faire, prenons calculer les racines cubiques ou élever au cube, d’utiliser les bons rouleaux, dans ce cas les modèles D et K, et d’utiliser une formule tellement magique qu’elle en devient mathématique : Logarithme ! !
Le logarithme est une fonction particulière qui est la réciproque de la fonction exponentielle, qui tend vers –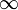 en zéro et vers +
en zéro et vers +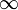 en +
en +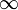 . Mais elle a surtout la propriété de rendre bien des calculs plus facile.
. Mais elle a surtout la propriété de rendre bien des calculs plus facile.
Par exemple la multiplication de deux termes prenons x et y ; le logarithme du produit de x et y est égale à la somme des logarithmes de chacun. En langage mathématique nous avons : 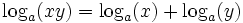 Dans notre cas elle utilise une autre spécificité : le logarithme d’un nombre, disons x, élevé à la puissance n est égale à n fois le logarithme de x:
Dans notre cas elle utilise une autre spécificité : le logarithme d’un nombre, disons x, élevé à la puissance n est égale à n fois le logarithme de x: 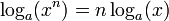 ainsi le logarithme d’un nombre élevé au cube est égale à trois fois le logarithme de ce nombre.
ainsi le logarithme d’un nombre élevé au cube est égale à trois fois le logarithme de ce nombre.
Et maintenant place à la technique, lorsqu’on utilise la partie coulissante et le curseur pour sélectionner un nombre sur le rouleau D, le deuxième curseur de l’autre côté de la partie coulissante marque sa valeur élevée au cube sur le rouleau K, mais par quelle magie ? En pratique le rouleau D suit une échelle logarithmique simple telle que :

Le rouleau K suit quant à lui une échelle graduée selon le logarithme de la racine cubique. (Mathématiquement 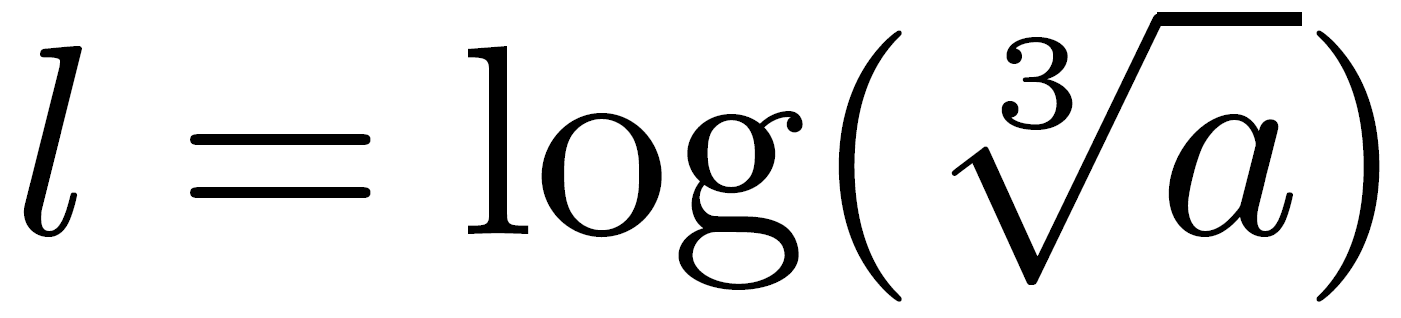 ) Ainsi, étant donné que les deux rouleaux sont placés de façon adéquate, nous avons l’équation :
) Ainsi, étant donné que les deux rouleaux sont placés de façon adéquate, nous avons l’équation : 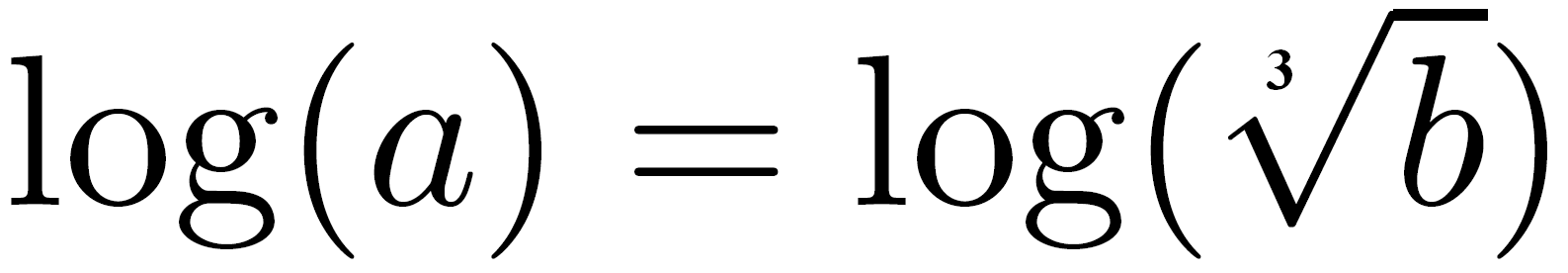 ainsi
ainsi 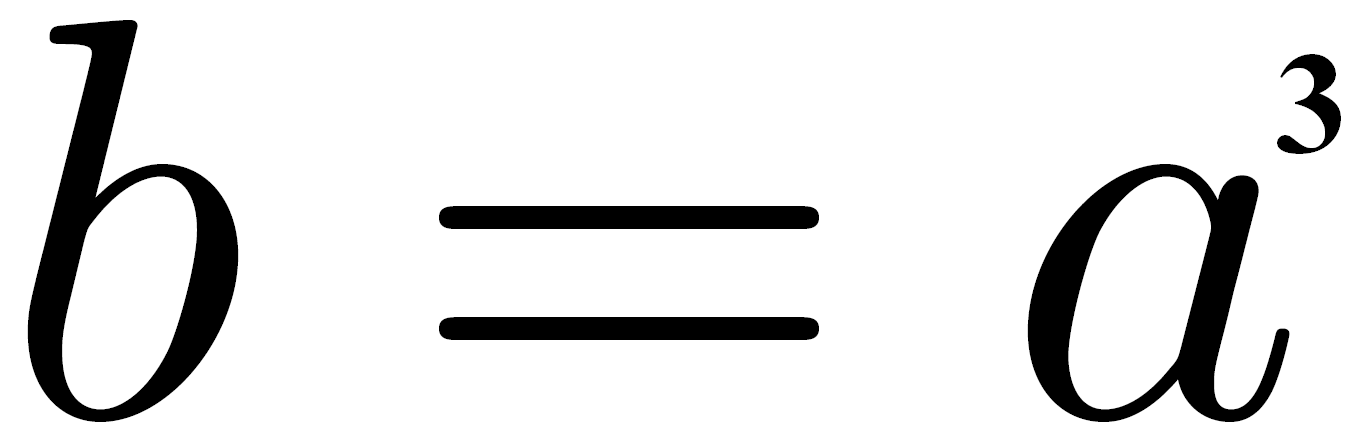 . Et bien sûr l’opération inverse est possible, il suffit de choisir un nombre sur le rouleau K et de regarder le résultat sur le rouleau D.
. Et bien sûr l’opération inverse est possible, il suffit de choisir un nombre sur le rouleau K et de regarder le résultat sur le rouleau D.
Malheureusement, ni la lunette d’observation, ni les règles de ce type ne sont autorisées durant les épreuves actuelles, bien des malins auraient étendu le concept de la réponse à la demande sur rouleau de papier.